----建议电脑阅读----为了弥补我那可悲的记忆力----
第8章 一元函数积分学的概念与计算
概念
(一)不定积分
1.原函数与不定积分
①存在x∈区间I,F’(x)=f(x),称F(x)是f(x)在区间I的一个原函数。
②其中F(x)+C是f(x)的全体原函数。
2.原函数(不定积分存在定理)
(1)连续函数f(x)必有原函数F(x)
证明

(2)含有第一类间断点和无穷间断点的函数f(x)在包含该间断点的区间内必没有原函数F(x)。
可去间断点:
证明

跳跃间断点
证明

无穷间断点
证明

(3)含有震荡间断点的函数可能有原函数,并且可推出,可导函数求导后的函数F’(x)=f(x)不一定是连续函数,但是如果有间断点,一定是第二类间断点。
3.积分函数的奇偶性、有界性、单调性、周期性
(1)连续的奇函数的一切原函数都是偶函数。
证明

(2)连续的偶函数的原函数有且仅有一个原函数是奇函数。
证明

(3)以T为周期的连续函数f(x),它在一个周期上的积分值与起点无关
证明

(4)以T为周期的连续函数f(x)的原函数以T为周期的充要条件
证明

(二)定积分
1.定积分的概念
①分割-》②近似-》③求和-》④取极限
∫abf(x)dx=n→∞limi=1∑nf(a+nb−ai)nb−a
主要掌握下面这个式子:
∫abf(x)dx=n→∞limi=1∑nf(a+n(b−a)⋅i)nb−a
将式子中的 (a, b) 特殊化为0, 1这两个数,得出的形式最为简单,也最利于解决问题:
∫01f(x)dx=n→∞limi=1∑nf(ni)n1
于是,“凑定积分定义”的步骤如下:
① 先提出 n1;
② 再凑出 ni;
③ 由于 ni=0+n1−0i,故 ni 可以读作“0到1上的 (x)”,且 n1=n1−0,读作“0到1上的 dx”
Tip:如果凑不出n1,则用“夹逼准则”
2.定积分存在定理
定积分存在定理,也称之为一元函数的(常义)可积性(“区间有限,函数有界”),与之后的“区间无穷,函数无界”的“反常”积分有所区别。
(1)定积分存在的充分条件
①连续;②单调;③有界,且只有有限个间断点(不包含无穷间断点、无界震荡);
(2)定积分存在的必要条件
可积函数必有界,即若定积分 ∫abf(x)dx存在,则f(x)在[a,b]上必有界
(3) 定积分的性质
①性质1(求区间长度):假设a<b,则∫abdx=b−a=L,其中L为区间[a,b]的长度.
②性质2(积分的线性性质):设k1,k2为常数,则∫[k1f(x)±k2g(x)]dx=k1∫f(x)dx±k2∫g(x)dx.
③性质3(积分的可加(拆)性):无论a,b,c的大小如何,总有∫acf(x)dx=∫abf(x)dx+∫bcf(x)dx.
④性质4(积分的保号性)若在区间[a,b]上f(x)≤g(x),则有∫abf(x)dx⩽∫abg(x)dx.
特别地,有∫abf(x)dx⩽∫ab∣f(x)∣dx.
⑤性质5(估值定理):设M,m分别是f(x)在[a,b]上的最大值和最小值,L为区间[a,b]的长度,则有mL⩽∫abf(x)dx⩽ML.
⑥性质6(中值定理):设f(x)在闭区间[a,b]上连续,则在[a,b]上至少存在一点ξ,使得 ∫abf(x)dx=f(ξ)(b−a) .
(三)变限积分
1.变限积分的概念
当x在[a,b]上变动时,对应于每一个x值,积分 ∫axf(t)dt 就有一个确定的值,因此 ∫axf(t)dt 是一个关于x的函数,记作 ϕ(x)=∫axf(t)dt(a≤x≤b),称函数 ϕ(x) 为变上限的定积分。同理可以定义变下限的定积分和上、下限都变化的定积分,这些都称为变限积分。事实上,变限积分就是定积分的推广。
2.变限积分的性质
f(x)可导->连续->可积->有界
(1) 若函数f(x)在[a,b]上可积,则函数F(x)=∫axf(t)dt在[a,b]上连续。
证明

(2) 若函数f(x)在[a,b]上连续,则函数F(x)=∫axf(t)dt在[a,b]上可导。
证明
如果函数f(x)在区间[a,b]上连续,则F(x)=∫axf(t)dt是f(x)在区间[a,b]上的一个原函数。
3.变限积分的求导公式
设 F(x)=∫axf(t)dt,其中 f(x) 在[a,b]上连续,可导函数φ1(x)和φ2(x)的值域在[a,b]上,则在函数φ1(x)和φ2(x)的公共定义域上,有

【注】我们称上面公式中的x为“求导变量“,t为“积分变量”,“求导变量”x只出现在积分的上、下限时才能使用变限积分求导公式,若“求导变量”x出现在被积函数中,必须通过恒等变形(比如变量代换等)将其移出被积函数,才能使用变限积分求导公式。
(四)反常积分
1.反常积分概念的通俗理解
破坏了积分区间的有限性或者破坏了被积函数的有界性
2.无穷区间上反常积分的概念与敛散性
一般来讲,在无穷区间上,函数f(X)趋向X轴的速度越快,则它的积分F(X)越容易收敛,如果趋向X轴的速度越慢,则越容易发散,但是F(x)收敛并不能推出f(x)的极限为0。
另外,反常积分 ∫−∞+∞f(x)dx 的定义为 ∫−∞+∞f(x)dx=∫−∞cf(x)dx+∫c+∞f(x)dx。若右边两个反常积分都收敛,则称反常积分 ∫−∞+∞f(x)dx 收敛,否则称为发散。
也就是说,要判断该类反常积分是否收敛,必须证明∫−∞cf(x)dx与∫c+∞f(x)dx同时收敛。
3.无界函数的反常积分的概念与敛散性
(1) 若 b 是 f(x) 的唯一瑕点,则无界函数 f(x) 的反常积分 ∫abf(x)dx定义为

若上述极限存在,则称反常积分 ∫abf(x)dx 收敛,否则称为发散。
(2) 若 c∈(a,b) 是 f(x) 的唯一瑕点,则无界函数 f(x) 的反常积分 ∫abf(x)dx 定义为

若上述右边两个反常积分都收敛,则称反常积分 ∫abf(x)dx 收敛,否则称为发散。
4.反常积分的敛散性判断

计算
(一)不定积分的积分法
1.基本积分公式
公式

2.凑微分法
详见书本
3.换元法
①三角函数代换
②恒等变形后作三角函数变换,当被积函数含有根式 ax2+bx+c时,可先化为以下三种形式,φ2(x)+k2、φ2(x)−k2、k2−φ2(x)
,再作三角函数变换.
③根式代换–当被积函数含有复杂根式时,一般让∗为t.
④倒代换–当被积函数分母的幂次比分子高两次及两次以上时,作倒代换,令x=t1
⑤复杂函数的直接变换——当被积函数中含有ax,ex,lnx,arcsinx,arctanx等时,可考虑直接令复杂函数等于t,值得指出的是,当lnx,arcsinx,arctanx与Pn(x)或eax作乘法时(其中Pn(x)为x的n次多项式),优先考虑分部积分法。 |
4.分部积分法
反、对、幂、指、三
裂项表格计算
5.有理函数的积分
(1) 定义:形如 ∫Qm(x)Pn(x)dx(其中 (n < m))的积分称为有理函数的积分,其中 (P_n(x)) 和 (Q_m(x)) 分别是 (x) 的 (n) 次多项式和 (m) 次多项式。
(2) 方法:先将 (Q_m(x)) 因式分解,再把 Qm(x)Pn(x) 拆成若干项最简有理分式之和。
(3) 分解的基本原则

(二)定积分的计算
1.定积分的换元积分法
2.定积分的分布积分法
1.区间再现公式
区间再现证明

例题

2.华里士公式









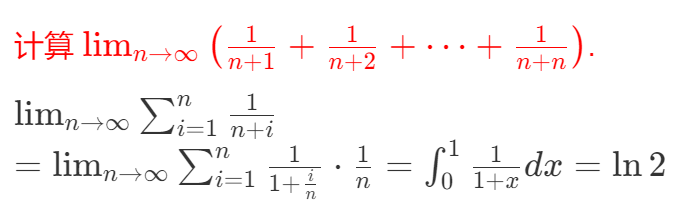


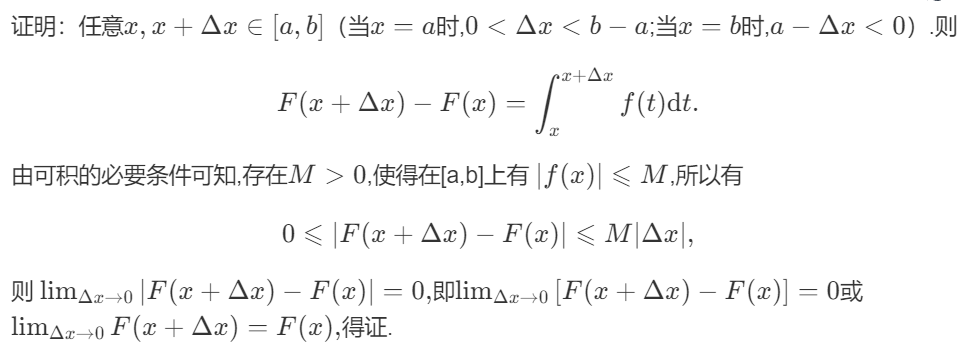




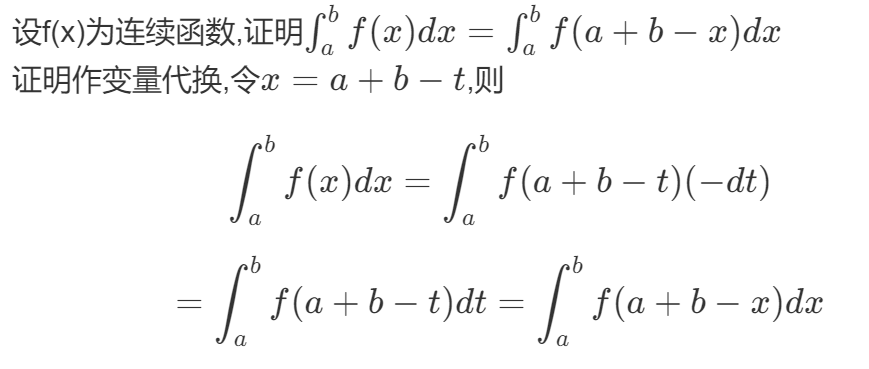
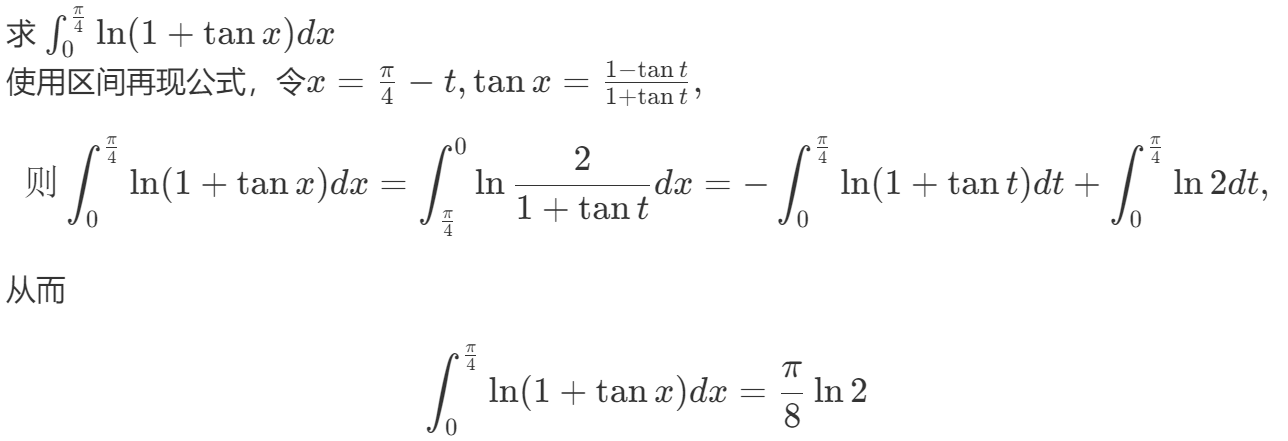
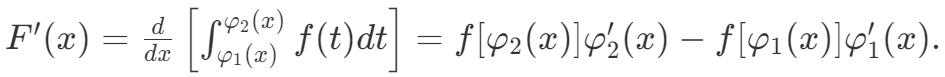
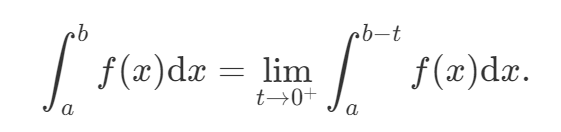
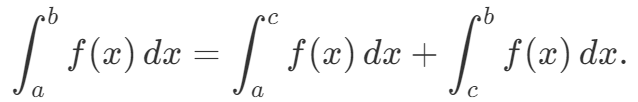



.jpg)