高数复习笔记

----建议电脑阅读----为了弥补我那可悲的记忆力----

第8章 一元函数积分学的概念与计算

概念

(一)不定积分

1.原函数与不定积分

①存在x∈区间I,F’(x)=f(x),称F(x)是f(x)在区间I的一个原函数。

②其中F(x)+C是f(x)的全体原函数。

2.原函数(不定积分存在定理)

(1)连续函数f(x)必有原函数F(x)

证明

(2)含有第一类间断点和无穷间断点的函数f(x)在包含该间断点的区间内必没有原函数F(x)。

可去间断点:

证明

跳跃间断点

证明

无穷间断点

证明

(3)含有震荡间断点的函数可能有原函数，并且可推出，可导函数求导后的函数F’(x)=f(x)不一定是连续函数，但是如果有间断点，一定是第二类间断点。

3.积分函数的奇偶性、有界性、单调性、周期性

(1)连续的奇函数的一切原函数都是偶函数。

证明

(2)连续的偶函数的原函数有且仅有一个原函数是奇函数。

证明

(3)以T为周期的连续函数f(x)，它在一个周期上的积分值与起点无关

证明

(4)以T为周期的连续函数f(x)的原函数以T为周期的充要条件

证明

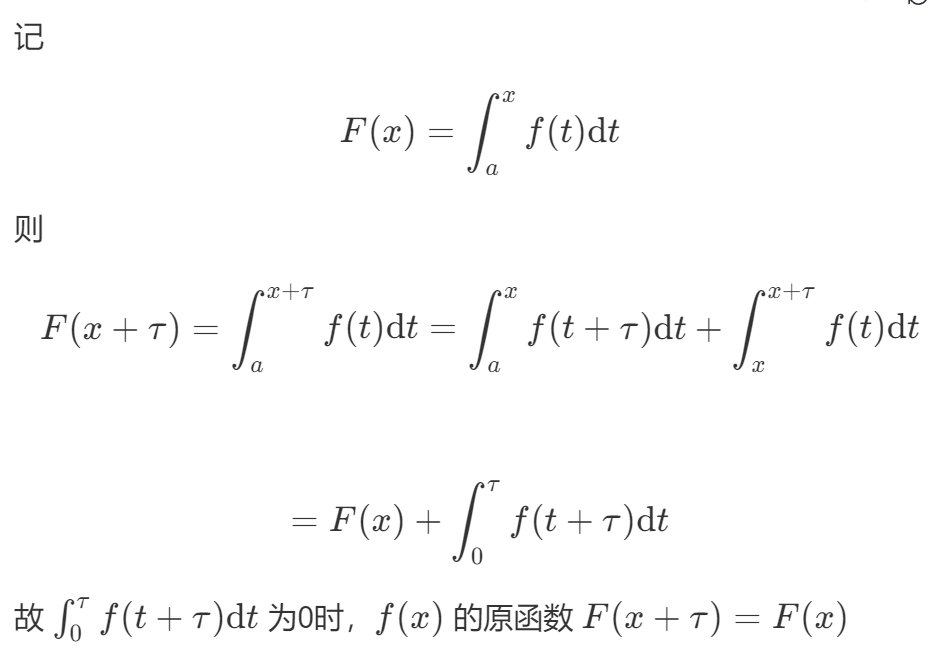
(二)定积分

1.定积分的概念

①分割-》②近似-》③求和-》④取极限

$$\int_a^bf(x)\mathrm{d}x=\lim_{n\to\infty}\sum_{i=1}^{n}f(a+\frac{b-a}{n}i)\frac{b-a}{n}$$

主要掌握下面这个式子：

$$\int_{a}^{b}f(x) \, dx = \lim_{n \to \infty} \sum_{i=1}^{n} f\left(a + \frac{(b - a) \cdot i}{n}\right) \frac{b - a}{n}$$

将式子中的 (a, b) 特殊化为0, 1这两个数，得出的形式最为简单，也最利于解决问题：

$$\int_{0}^{1}f(x)\mathrm{d}x=\lim_{n\to\infty}\sum_{i=1}^{n}f\left(\frac{i}{n}\right)\frac{1}{n}$$

于是，“凑定积分定义”的步骤如下：

① 先提出 $\frac{1}{n}$；
② 再凑出 $\frac{i}{n}$；
③ 由于 $\frac{i}{n}=0+\frac{1-0}{n}i$，故 $\frac{i}{n}$ 可以读作“0到1上的 (x)”，且 $\frac{1}{n}=\frac{1-0}{n}$，读作“0到1上的 $\mathrm{d}x$”
Tip:如果凑不出$\frac{1}{n}$,则用“夹逼准则”

• 例题 1
• 例题 2
• 例题 3

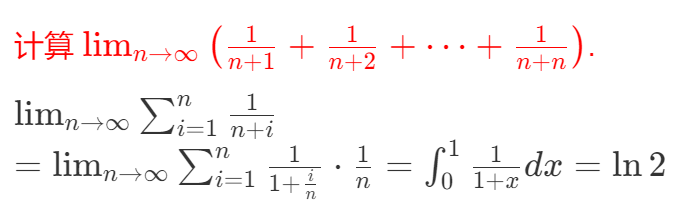
2.定积分存在定理

定积分存在定理，也称之为一元函数的(常义)可积性(“区间有限，函数有界”)，与之后的“区间无穷，函数无界”的“反常”积分有所区别。

(1)定积分存在的充分条件

①连续；②单调；③有界，且只有有限个间断点(不包含无穷间断点、无界震荡)；

(2)定积分存在的必要条件

可积函数必有界,即若定积分 $\int_{a}^{b}f(x)\mathrm{d}x$存在,则f(x)在[a,b]上必有界

(3) 定积分的性质

①性质1(求区间长度)：假设$a<b$,则$\int _{a}^{b}dx=b-a=L$,其中L为区间[a,b]的长度.
②性质2(积分的线性性质)：设$k_1, k_2$为常数，则$\int [k_1f(x)\pm k_2g(x)]dx=k_1\int f(x)dx \pm k_2\int g(x)dx.$
③性质3(积分的可加(拆)性)：无论a,b,c的大小如何,总有$\int_{a}^{c}f(x)\mathrm{d}x=\int_{a}^{b}f(x)\mathrm{d}x+\int_{b}^{c}f(x)\mathrm{d}x.$
④性质4(积分的保号性)若在区间[a,b]上f(x)≤g(x),则有$\int_{a}^{b} f(x)\mathrm{d}x\leqslant\int_{a}^{b} g(x)\mathrm{d}x.$
特别地,有$\left|\int_{a}^{b} f(x)\mathrm{d}x\right|\leqslant\int_{a}^{b}\left|f(x)\right|\mathrm{d}x.$
⑤性质5(估值定理)：设M,m分别是f(x)在[a,b]上的最大值和最小值,L为区间[a,b]的长度,则有$mL\leqslant \int_{a}^{b}f(x)\mathrm{d}x \leqslant ML$.
⑥性质6(中值定理)：设f(x)在闭区间[a,b]上连续,则在[a,b]上至少存在一点ξ,使得 $\int_{a}^{b}f(x)\mathrm{d}x=f(\xi)(b-a)$ .

(三)变限积分

1.变限积分的概念

当x在[a,b]上变动时，对应于每一个x值，积分 $\int_{a}^{x} f(t) \, dt \,$ 就有一个确定的值，因此 $\int_{a}^{x} f(t) \, dt \,$ 是一个关于x的函数，记作 $\phi(x) = \int_{a}^{x} f(t) \, dt \, (a \leq x \leq b)$，称函数 $\phi(x)$ 为变上限的定积分。同理可以定义变下限的定积分和上、下限都变化的定积分，这些都称为变限积分。事实上，变限积分就是定积分的推广。

2.变限积分的性质

f(x)可导->连续->可积->有界
(1) 若函数f(x)在[a,b]上可积，则函数$F(x)=\int_{a}^{x}f(t)dt$在[a,b]上连续。

证明

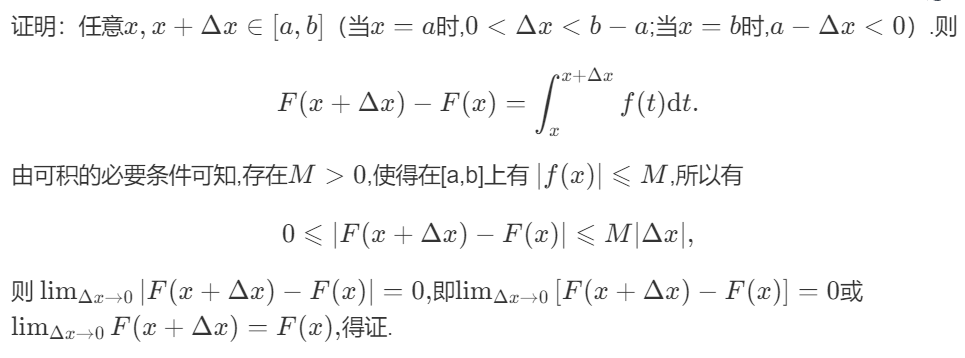
(2) 若函数f(x)在[a,b]上连续，则函数$F(x)=\int_{a}^{x}f(t)dt$在[a,b]上可导。

证明

如果函数f(x)在区间[a,b]上连续，则$F(x)=\int_{a}^{x}f(t)dt$是f(x)在区间[a,b]上的一个原函数。

3.变限积分的求导公式

设 $F(x)=\int_{a}^{x}f(t)dt$,其中 $f(x)$ 在$[a,b]$上连续,可导函数$\varphi _{1}(x)$和$\varphi _{2}(x)$的值域在$[a,b]$上,则在函数$\varphi _{1}(x)$和$\varphi _{2}(x)$的公共定义域上,有

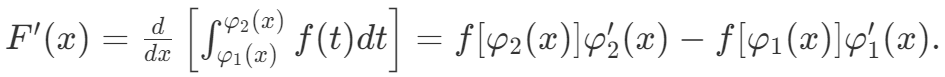
【注】我们称上面公式中的x为“求导变量“，t为“积分变量”，“求导变量”x只出现在积分的上、下限时才能使用变限积分求导公式,若“求导变量”x出现在被积函数中,必须通过恒等变形(比如变量代换等)将其移出被积函数，才能使用变限积分求导公式。

(四)反常积分

1.反常积分概念的通俗理解

破坏了积分区间的有限性或者破坏了被积函数的有界性

2.无穷区间上反常积分的概念与敛散性

一般来讲，在无穷区间上，函数f(X)趋向X轴的速度越快，则它的积分F(X)越容易收敛，如果趋向X轴的速度越慢，则越容易发散，但是F(x)收敛并不能推出f(x)的极限为0。
另外，反常积分 $\int_{-\infty}^{+\infty} f(x)dx$ 的定义为 $\int_{-\infty}^{+\infty} f(x)dx = \int_{-\infty}^{c} f(x)dx + \int_{c}^{+\infty} f(x)dx$。若右边两个反常积分都收敛，则称反常积分 $\int_{-\infty}^{+\infty} f(x)dx$ 收敛，否则称为发散。
也就是说，要判断该类反常积分是否收敛，必须证明$\int_{-\infty}^{c} f(x)dx$与$\int_{c}^{+\infty} f(x)dx$同时收敛。

3.无界函数的反常积分的概念与敛散性

(1) 若 $b$ 是 $f(x)$ 的唯一瑕点，则无界函数 $f(x)$ 的反常积分 $\int_{a}^{b} f(x)\mathrm{d}x$定义为

若上述极限存在，则称反常积分 $\int_{a}^{b} f(x)\mathrm{d}x$ 收敛，否则称为发散。

(2) 若 $c \in (a,b)$ 是 $f(x)$ 的唯一瑕点，则无界函数 $f(x)$ 的反常积分 $\int_{a}^{b} f(x) \, dx$ 定义为

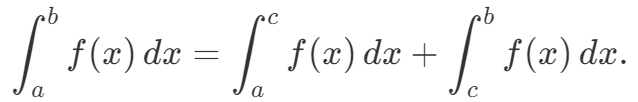
若上述右边两个反常积分都收敛，则称反常积分 $\int_{a}^{b} f(x) \, dx$ 收敛，否则称为发散。

4.反常积分的敛散性判断

• 例题 1
• 例题 2
• 例题 3

计算

(一)不定积分的积分法

1.基本积分公式

公式

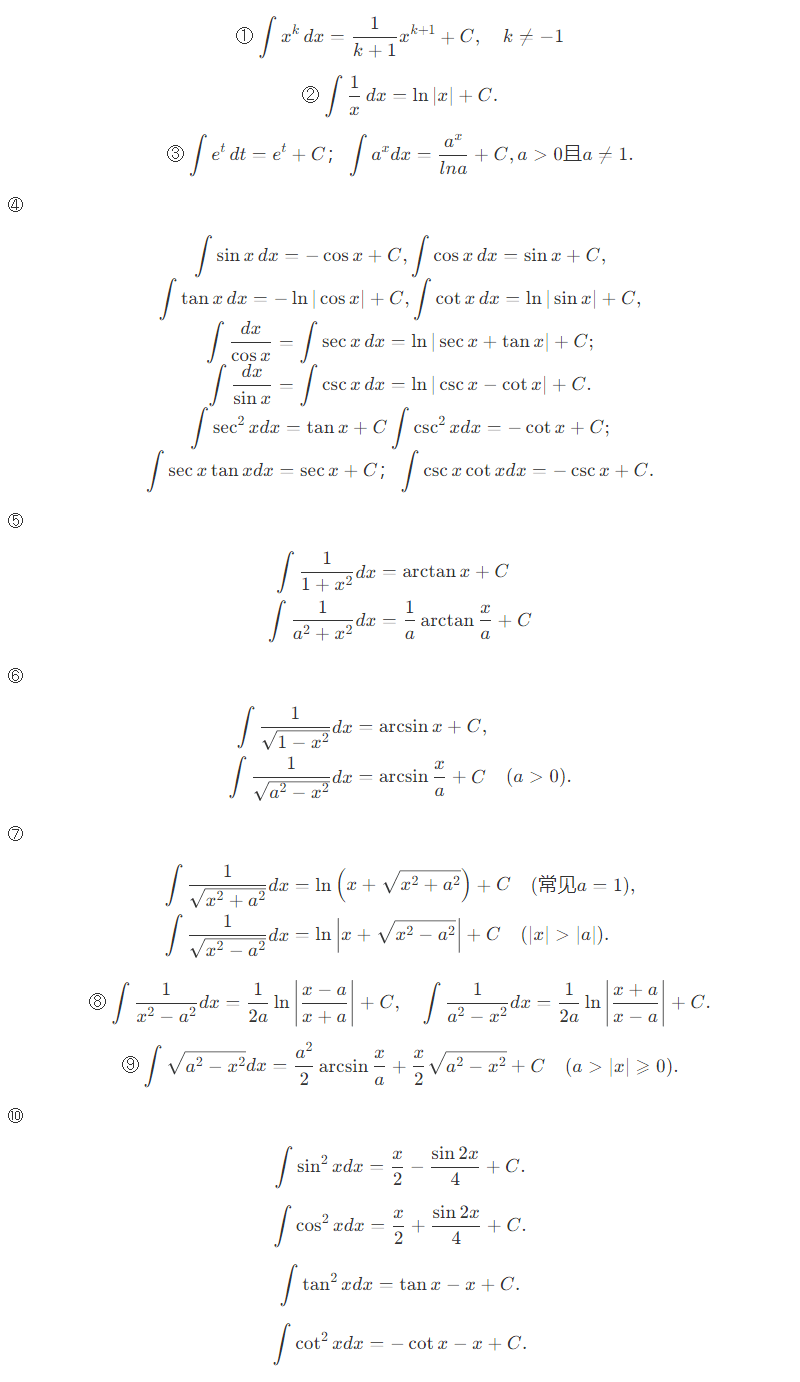
2.凑微分法

详见书本

3.换元法

①三角函数代换
②恒等变形后作三角函数变换，当被积函数含有根式 $\sqrt{ax^2+bx+c}$时,可先化为以下三种形式,$\sqrt{\varphi^2(x)+k^2}、 \sqrt{\varphi^2(x)-k^2}、\sqrt{k^2-\varphi^2(x)}$
,再作三角函数变换.
③根式代换–当被积函数含有复杂根式时，一般让$\sqrt{*}$为t.
④倒代换–当被积函数分母的幂次比分子高两次及两次以上时，作倒代换,令x=$\frac{1}{t}$
⑤复杂函数的直接变换——当被积函数中含有$a^{x}$，$e^{x}$，$\ln x$，$\arcsin x$，$\arctan x$等时，可考虑直接令复杂函数等于t，值得指出的是，当$\ln x$，$\arcsin x$，$\arctan x$与$P_{n}(x)$或$e^{ax}$作乘法时（其中$P_{n}(x)$为$x$的$n$次多项式），优先考虑分部积分法。 |

4.分部积分法

反、对、幂、指、三
裂项表格计算

5.有理函数的积分

(1) 定义：形如 $\int \frac{P_n(x)}{Q_m(x)}\,\mathrm{d}x$（其中 (n < m)）的积分称为有理函数的积分，其中 (P_n(x)) 和 (Q_m(x)) 分别是 (x) 的 (n) 次多项式和 (m) 次多项式。

(2) 方法：先将 (Q_m(x)) 因式分解，再把 $\frac{P_n(x)}{Q_m(x)}$ 拆成若干项最简有理分式之和。

(3) 分解的基本原则

(二)定积分的计算

1.定积分的换元积分法

2.定积分的分布积分法

1.区间再现公式

区间再现证明

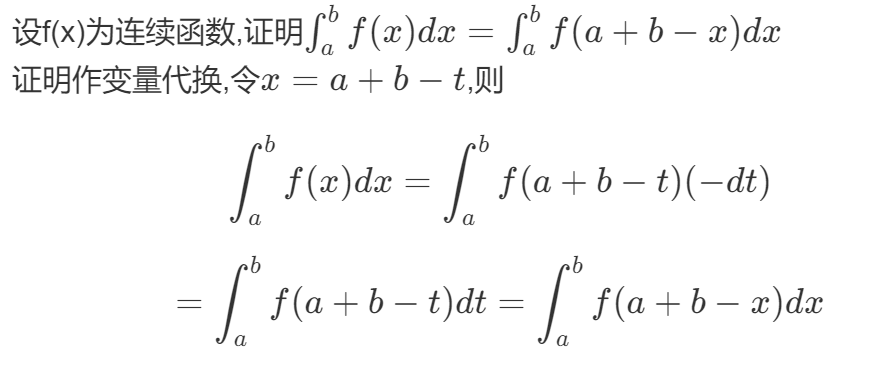
例题

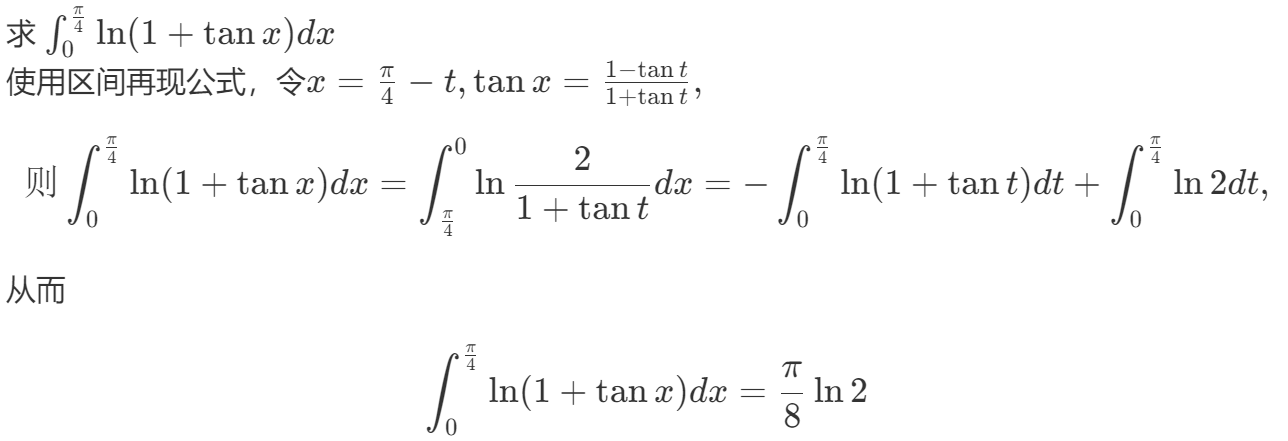
2.华里士公式