用于期末考试的临时抱佛脚= w =

算法的基本概念

算法是求解问题的一系列计算步骤，用来将输入转换成输出结果。

算法的时间复杂度

算法所耗费的时间应是算法中每条语句的执行时间之和，而每条语句的执行时间就是该语句的执行次数(频度)与该语句执行一次所需时间的乘积。

渐进符号

O符号:渐进上界(最坏情况)。用O(g(n))表示，其中g(n)是算法运行时间的一个上界。例如，如果一个算法的时间复杂度是O(n)，那么它的运行时间不会超过n的线性函数。

Ω符号:渐进下界。用Ω(g(n))表示，其中g(n)是算法运行时间的一个下界。如果一个算法的时间复杂度是Ω(n)，那么它的运行时间至少是n的线性函数。

Θ符号:同阶。表示算法的平均情况时间复杂度。用Θ(g(n))表示，其中g(n)是算法运行时间的紧确界。如果一个算法的时间复杂度是Θ(n)，那么它的运行时间在最坏情况和最好情况下都是n的线性函数。

p13

Master方法

p1
p2

分而治之

(1)该问题的规模缩小到一定程度就可以解决。
(2)该问题可以分为若干个规模较小的相同问题，即该问题具有最优子结构性质。
(3)利用该问题分解出的子问题的解可以合并为该问题的解。
(4)利用该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共子问题。

总结:子问题相互独立，并与原问题性质一样。

分治法查找最值问题

p9

1
2
3
4
5
6
7
8
9
10
11
int max(int A[],int low,int high){
	if(low==high){
		return A[low];
	}
	int mid=(low+high)/2;
	int a=max(A,low,mid);
	int b=max(A,mid+1,high);
	if(a>b){
		return a;
	}else return b;
}

分治法查找元素

p10

1
2
3
4
5
6
7
8
9
10
11
12
int com(int A[], int low, int high, int x) {
    if (low == high) {
        if (A[low] > x) {
            return 1;
        }else return 0;
    } else {
        int mid = (low + high) / 2;
        int a=com(A, low, mid, x);
        int b=com(A, mid + 1, high, x);
        return a+b;
    }
}

归并排序的核心代码

分解 -> 求解子问题 -> 合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void MergeSort(int arr[],int left,int right){
	if(left>=right) return;
	int mid=(left+right)/2;
	MergeSort(arr,left,mid);
	MergeSort(arr,mid+1,right);
	int begin=0,l=left,end=mid+1;
	while(l<=mid && end<=right){
		if(arr[l]<arr[end]) tmp[begin++]=arr[l++];
		else tmp[begin++]=arr[end++];
	}
	while(l<=mid)tmp[begin++]=arr[l++];
	while(end<=right)tmp[begin++]=arr[end++];
	for(int i=left,j=0;i<=right;i++,j++)arr[i]=tmp[j];
}

归并排序时间复杂度

T(n)=O(1)          n<=1
T(n)=2T(n/2)+O(n)  n>1

快速排序核心代码

分解 -> 求解子问题 -> 合并

1
2
3
4
5
6
7
8
9
10
11
12
13
void QuickSort(int arr[],int left,int right){
	if(left>=right)return;
	int mid=arr[(left+right)/2],l=left-1,r=right+1;
	while(l<r){
		do l++;while(arr[l]<mid);
		do r--;while(arr[r]>mid);
		if(l<r){
			swap(arr[l],arr[r])
		}
	}
	QuickSort(arr,left,r);
	QuickSort(arr,r+1,right);	
}

快速排序时间复杂度

T(n)=O(1)          n<=1
T(n)=2T(n/2)+O(n)  n>1

大整数乘法

分为3个子问题

Strassen 矩阵乘法

8个子问题简化为7个子问题

棋盘覆盖

p11

备忘录算法与动态规划算法的区分

   动态规划算法是备忘录方法的变形，它通过分治思想对原问题进行分解，以存储子问题的解的方式解决冗余计算，并采用自底向上的递推方式获取问题的最优解。
   递推方式是自底向上递归求解，而备忘录方法是自顶向下递归求解。当一个问题的所有子问题都至少要解一次时，可以考虑使用动态规划算法。当子问题空间中的部分子问题不需要求解时，可以考虑使用备忘录方法。

动态规划的基本步骤

(1)找出最优解的性质，并刻画其结构特征。
(2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
(4)根据计算最优值时得到的信息，构造最优解。

动态规划算法的基本要素

(1)最优子结构性质。
(2)子问题重叠性质。

矩阵连乘问题

分析最优解的结构->递归地定义最优值->计算最优值(原问题的最优解包含子问题的最优解)

矩阵A1A2A3A4有着五中不同的完全加括号的方式:(A1(A2(A3A4))),(A1((A2A3)A4)),((A1A2)(A3A4)),((A1(A2A3))A4),(((A1A2)A3)A4)。每一种完全加括号的方式对应于一个矩阵连乘积的计算次序，这决定这矩阵相乘所需要的计算量。

最长公共子序列问题

		{			0				i,j=0
c[i][j]={		c[i-1][j-1]+1		i,j>0 xi=yi
		{max{c[i][j-1],c[i-1][j]}	i,j>0,xi!=yi

p3

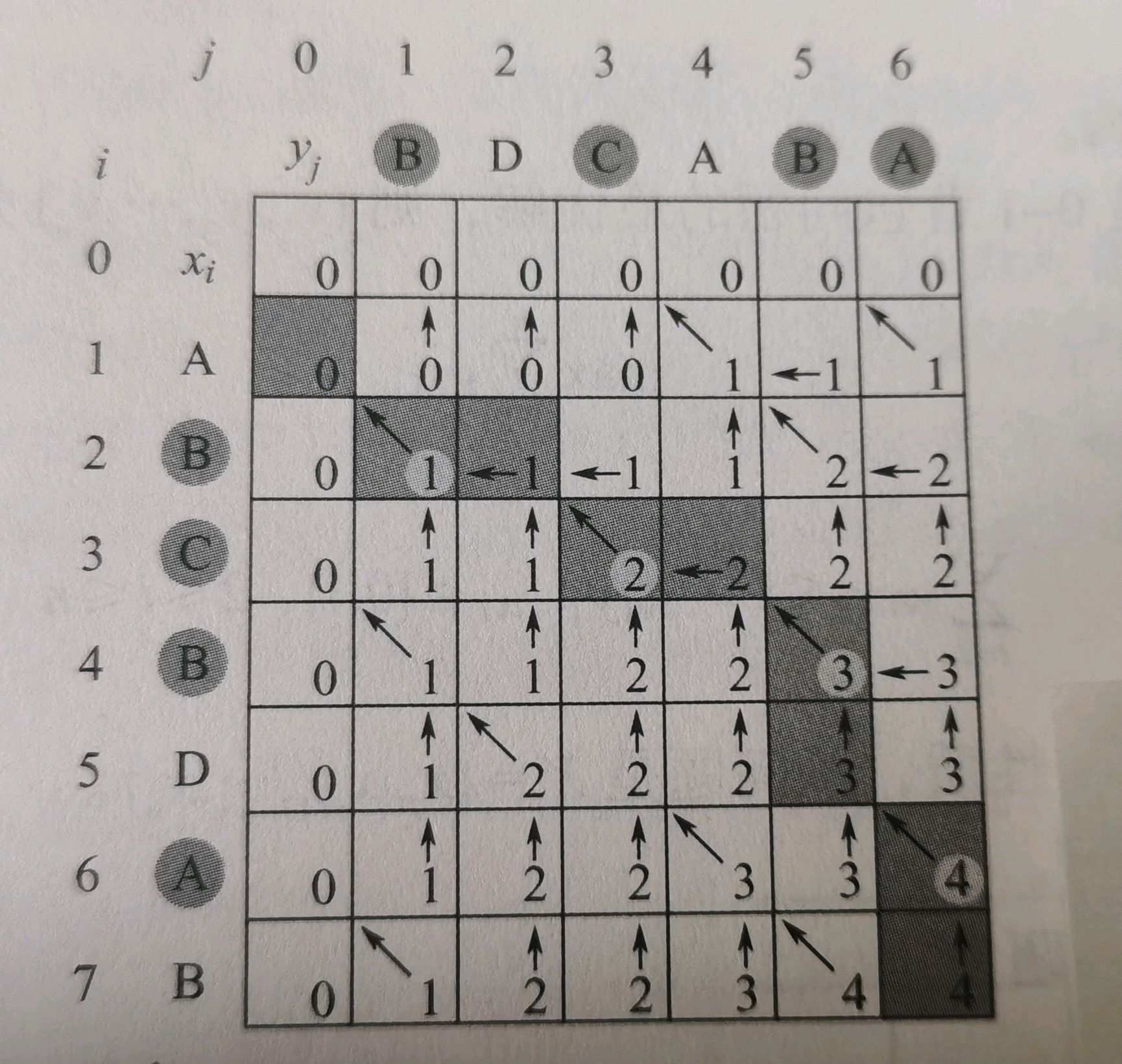
01背包问题可以用分支限界、回溯、动态规划方式

01背包问题题例

p14

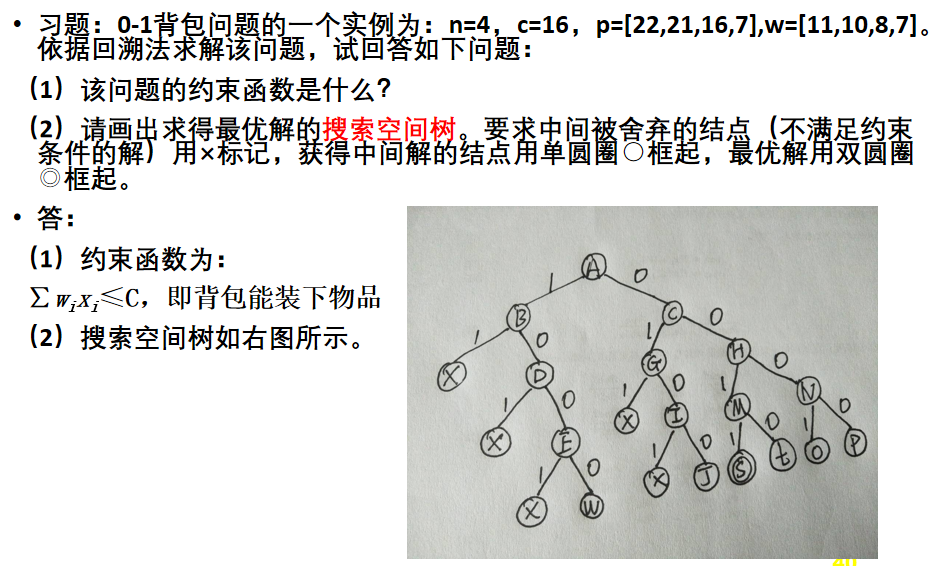
背包问题可用贪心

最大子段和问题可采用分治与动态规划算法

p12

凸多边形最优三角部分

采用动态规划的方式: 分析最优解的结构->递归定义最优值->自底向上计算最优值。 (最优子问题、重叠子问题)

贪心算法的基本思想

(1)最优子结构性质
(2)贪心选择性质

活动安排问题

(1)最早开始时间，增大资源利用率。
(2)最早结束时间，使下一活动尽早开始。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void sort(int begin[],int end[],int n){
	int tmp;
	for(int i=0;i<n-1;i++){
		for(int j=i+1;j<n;j++){
			if(end[i]>end[j]){
				tmp=begin[i];
				begin[i]=begin[j];
				begin[j]=tmp;
				tmp=end[i];
				end[i]=end[j];
				end[j]=tmp;
			}
		}
	}
}
int action(int begin[],int end[],bool flag[],int n){
	flag[0]=1;
	int j=0,count=1;
	cout<<begin[0]<<" "<<end[0]<<endl;
	for(int i=1;i<n;i++){
		if(begin[i]>=end[j]){
			flag[i]=1;
			j=i;
			count++;
			cout<<begin[i]<<" "<<end[i]<<endl;
		}else {
			flag[i]=0;
		}
	}
	return count;
}

最优装载问题

(1)选择重量小的先装，所以首先需排序。
(2)不断装载，则需要循环;要输出最优装载方案，则需进行装载记录。

1
2
3
4
5
6
7
8
9
void Loading(int x[],Type w[],Type c,int n){
	int *t=new int [n+1];
	Sort(w,t,n);
	for(int i=1;i<=n;i++) x[i]=0;
	for(int i=1;i<=n && w[t[i]]<=c;i++){
		x[t[i]]=1;
		c-=w[t[i]];
	}
}

哈夫曼树由贪心算法构造

回溯法:子集树、排列树

子集树:当所给问题是从n个元素的集合中找出满足某性质的子集时，相应的解空间树成为子集树。
排列树:当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。

符号三角形问题、01背包问题能用子集树解决

旅行商、售货员问题用排列树解决

其中旅行商问题是从求最小值到求最小堆

约束函数剪枝关注问题的可行性，而限界函数剪枝关注问题的最优性

最大团问题内容

p15

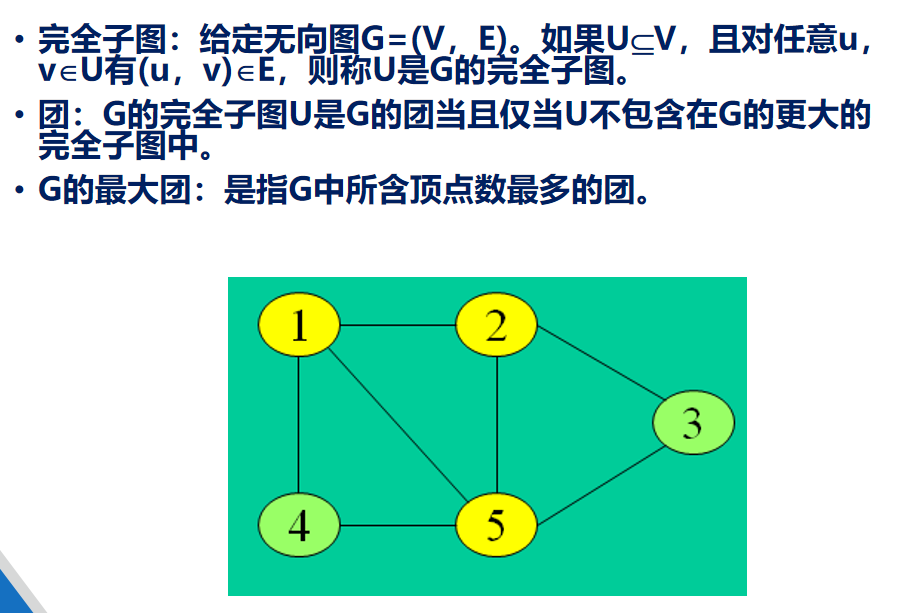
最大团问题题例

p16
p17
p18

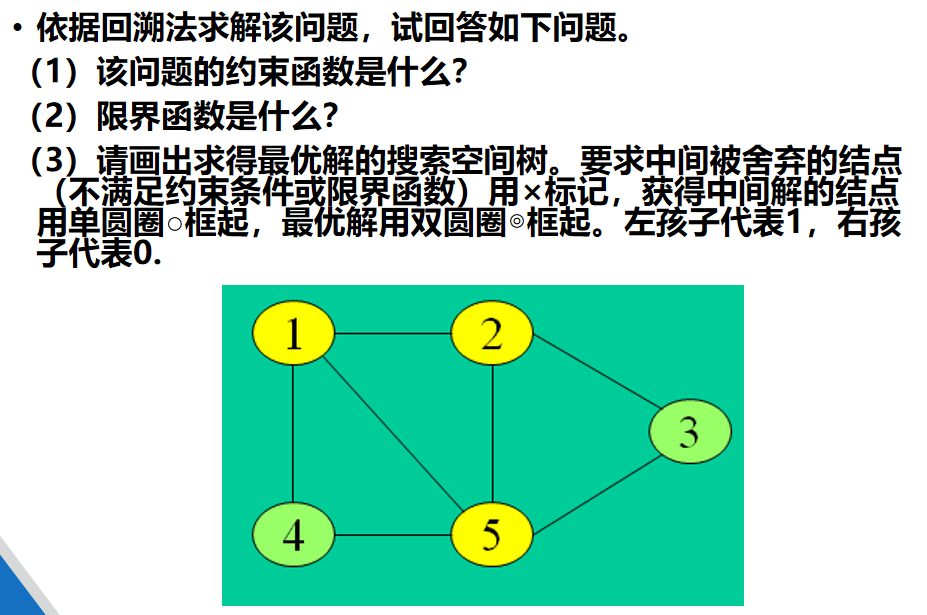
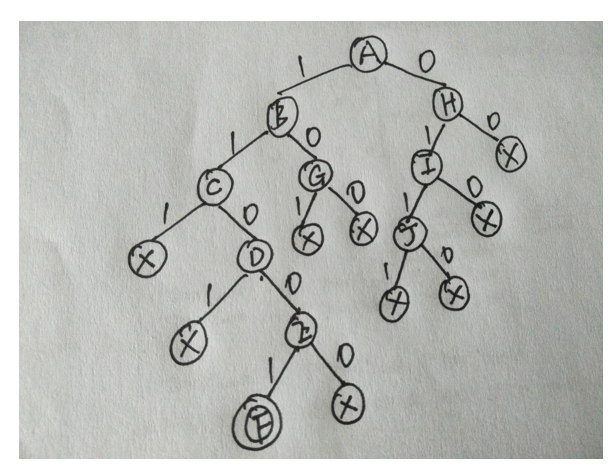
分支限界法基本思想

在分支限界法中，每一个活结点只有一次机会成为扩展节点。活结点一旦成为扩展节点，就一次性产生其所有孩子节点。

分支界限法两种方式

队列式分支限界法:将活结点表组织成一个队列，并按队列的先进先出原则选择下一个结点作为当前扩展结点。

优先队列式分支限界法:将活结点表组织成一个优先队列，并按优先队列中规定的结点优先级优先选取优先级最高的结点最为当前扩展结点。

分支限界法与回溯法的区别:

(1)求解目标不同:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。

(2)搜索方式不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。

队列式分支限界法的算法框架

(1)初始化解空间树的根结点(第一个活结点)和一个空队列。
(2)根结点入队列
(3)若队列不为空，则循环执行以下各步
		出队一个结点P(当前扩展结点)
		while(P的所有满足约束条件的孩子结点T)
		{
			若T不是叶子结点
			则将T加入队列
			否则用于更新最优值及记录该叶子结点
		}
(4)根据记录的叶子结点构造最优解

优先队列式分支限界法的算框架

(1)初始化解空间树的根结点(当前扩展结点)P和一个空堆
(2)while(当前扩展结点P不是叶子结点)
	{
		while(P的所有满足约束条件的孩子结点T)
		{
			将T插入堆
		}
		堆顶元素赋值给P;
	}
(3)根据当前扩展结点P求最优值并构造最优解